Problem Solving Basis - Dijkstra

Find shortest path, given starting node, with positive path distance.

Idea

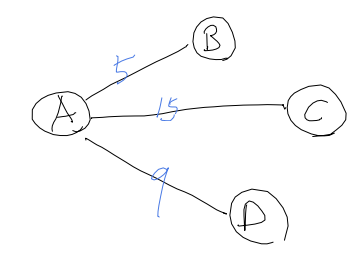
Suppose you are at vertex A. Three questions to ask:

• Q1. Which path is guaranteed to be shortest?
• Q2. If so, where should we go next?
• Q3. Which vertex(node) is not necessary to go as we move further?

For Q1, only path A-B is guaranteed to be shortest. Other routes, A-C and A-D are not, as some path from vertex B might be shorter, as follows.

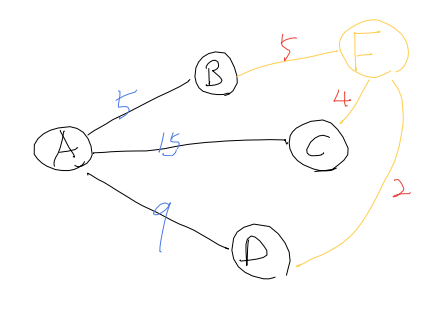
For Q2, we should follow shortest from all path recognized, and search from that shortest path’s destination.

For Q3, It is not necessary to visit back to the shortest path from Q2. So if any vertex calls that node, we may skip it.

How To

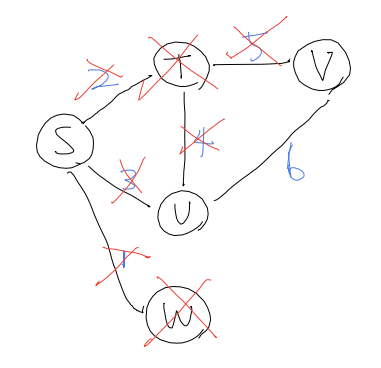
Here is our example.

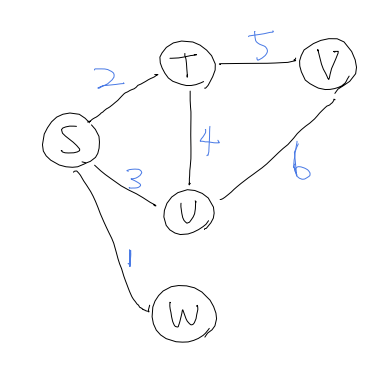
Initialization

distance/ visited array

Let the starting point be S. Then we may set up an distance array from S. Initializing all by INF value, and set dist starting point to be 0.

              S   T   U   V   W 
dist from S   0  INF INF INF INF
visited       T   F   F   F   F

priority queue

Our algorithm need to search from shortest distance from the source (to any of vertex). To do this efficiently, priority queue will be used.

Updates

Step 1

Start from S. S has 3 adjacent vertices T, V, W.

So among paths S-T, S-V, S-W, S-W is the shortest, and this path will be popped up.

We may mark W as visited, since there will be no other paths that will lead to W. (since we popped the shortest!)

How about T and V? They need to be reconsidered, as there might be some other path from W. So we just update distance array, keeping visited array as before.

              S   T   U   V   W 
dist from S   0  *2  *3  INF *1
visited       T   F   F   F   F

step 2

Start from W. No other vertex is linked. so we just skip. W is marked complete.

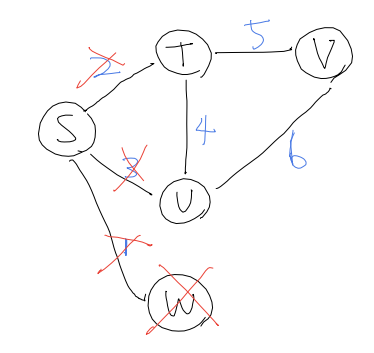
              S   T   U   V   W
dist from S   0   2   3  INF  1
visited       T   F   F   F   *T

step 3

Start from T. Two paths available: T-U, T-V.

• T-U: total distance is 6, (dist S to T + T to U) and we have already marked S-U (dist[U] = 3) is shorter. no updates.
• T-V: initial update. S to T + T to V is 7

T is marked visited.

              S   T   U   V   W
dist from S   0   2   3  *7   1
visited       T   T   F   F   T

step 4

Start from U. single path available: U-V.

• U-V: total distance is 9, (dist S to T + T to U) and we have already marked S-V (dist[U] = 7) is shorter. no updates.

U is marked visited.

              S   T   U   V   W
dist from S   0   2   3   7   1
visited       T   T  *T   F   T

step 5

Finally, V. V is marked visited.

              S   T   U   V   W
dist from S   0   2   3   7   1
visited       T   T   T  *T   T

Template Code

python (with heapq)

def dijkstra(start):
  q = []
  dist[start] = 0
  heapq.heappush(q, (0, start))

  while q:
    cur_cost, cur_node = heapq.heappop(q)

    for (node, cost) in graph[cur_node]:
      next_cost = cur_cost + cost
      if cost < dist[node]:
        dist[node] = next_cost
        heapq.heappush(q, (next_cost, node))

https://github.com/carrtesy/CodingTest_python/blob/main/shortest_path/dijkstra_template.py

cpp: https://github.com/dongminkim0220/Problem-Solvings/blob/master/templates/cpp/dijkstra.cpp

#

Complexity Analysis

V nodes, and E edges.

• Time: all edges are visited at most once, and those edge information is managed by priority queue. So, $ O(ElogE) = O(ElogV) $

• Space: $ O(

  V

  ) $ for distance/visited matrix, and also priority queue

Problems to Solve

• basics: https://www.acmicpc.net/problem/1753