Problem Solving Basis - Topological Sort

How can we program the computer to wear socks first, and then shoes?

Idea

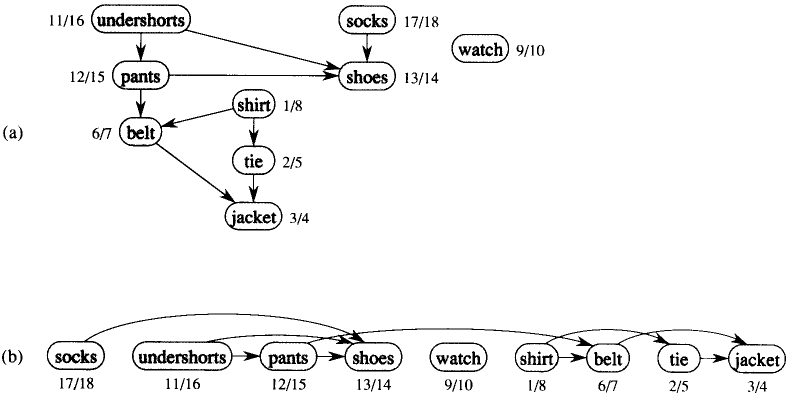
Image from: http://personal.kent.edu/~rmuhamma/Algorithms/MyAlgorithms/GraphAlgor/topoSort.htm

Topological Sort sorts the order. To sort something, we need something to compare. In this kind of problem, that order is given as priority. For example, socks and then shoes.

How To

Data structure

Input is given in the form of “A should be done earlier than B”.

In this sense, we may think of structure something like:

A -> B -> C -> D ...

For this linked structure, we will use directed graph.

So our graph in adjacency list will be:

socks       | -> shoes
undershorts | -> shoes -> pants
pants		| -> shoes -> belt
shoes		|
watch		|
shirt		| -> belt -> tie
belt		| -> jacket
tie			| -> jacket
jacket		|

What should be done first

Something that should be done first has no prior things to do.

In other words, If some task (like shoes) has prior things (socks) that should be done first, then that should not be done right now.

So, How can we think of the condition “no prior thing to do” in our graph data structure?

Right, Indegree of that node should be zero.

Algorithm

Firstly, push the nodes with indegree of 0 to the queue.

Secondly, do the task.

Third, when task is done, delete the task, with its edges to other tasks. Repeat from the first.

Complexity Analysis

Graph takes E edges, V vertices.

• Time: V nodes are into queue, and E edges are checked and deleted, so O(V+E)
• Space: O(E) for adjacency list

Template Code

cpp: https://github.com/dongminkim0220/Problem-Solvings/blob/master/templates/cpp/topological_sort.cpp

Problems to Solve

• basics: https://www.acmicpc.net/problem/2252